Аллавердян В.В. — директор ООО «ОКК «ИКР-Консультант»
Бабенко Р.В., к.э.н., Председатель правления Ростовского РО РОО
Свирепо О.А. — оценщик
Забелина А.В. — помощник директора ООО «ОКК «ИКР-Консультант»
С увеличением площади незастроенного земельного участка в текущих условиях обычно наблюдается фактическое снижение ставок арендной платы. Обоснование поправки на снижение ставок во многих отчетах делается «экспертно». В то же время действует прямое указание об обосновании существенной информации для определения стоимости объекта оценки, если используется экспертное суждение оценщика или привлеченного оценщиком специалиста (эксперта). Таким образом, должны быть описаны условия, при которых оцениваемые характеристики могут достигать тех или иных значений [1, п. 19, абз. 4].
Попытка проведения опросов зачастую приводит к достаточно большому разбросу мнений экспертов [2]. Для снижения разброса можно пойти на уменьшение количества использованных мнений. Однако этот вариант может привести к увеличению погрешности расчетов.
Корректировки, рассчитываемые методом парных продаж, обычно строятся на линейной зависимости, которая не всегда корректно отражает экономическую природу явлений при количестве факторов ценообразования более одного, что также не улучшает качество оценки.
В настоящей статье авторы предлагают практическое применение алгоритма определения корректировок для оценки нетипичных объектов с использованием математических методов при выполнении двух условий:
1) существует достаточное количество информации об объектах сравнения (шесть и более);
2) расчет корректировки методом парных продаж дает высокую погрешность.
При помощи предлагаемой последовательности действий можно построить математические модели, которые с наибольшей вероятностью позволят вычислить необходимые параметры оцениваемого объекта.
Для удобства изложения материала алгоритм рассматривается на конкретном примере.
Перед оценщиком поставлена задача расчета ставки годовой арендной платы для двух незастроенных земельных участков (земли поселений). Сложность данной задачи заключается в том, что площади земельных участков существенно отличаются от обычно участвующих в обороте и составляют соответственно 60,0444 и 235,0555 га. Согласно имеющимся в договорном отделе договорам аренды земельных участков, медиана площади составляет 1,3 га.
Типичным вариантом использования подобных земельных участков с учетом подобных условий расчетов является комплексная застройка. В текущих условиях на региональных рынках заниматься инвестированием с использованием таких площадей может достаточно немногочисленная группа застройщиков. Таким образом, при снижении количества потенциальных инвесторов, имеющих потребность в объекте нетипично большого масштаба, возникает ситуация, называемая «рынок покупателя». Выставление земельного участка одним большим лотом с одной стороны социально значимо для муниципалитета (обычно инвестору предлагается «нагрузка» в виде социальных объектов), а с другой стороны — выгодно на конкурентном рынке инвестору (меньше конкурентов и снижение ставок в борьбе, так как муниципалитету политически невыгодно снимать лот с торгов за отсутствием спроса). Приведенные выше пояснения необходимы для раздела отчета «Анализ наиболее эффективного использования».
Наш предыдущий опыт оценки показал, что площадь является одним из основных ценообразующих факторов, и удельная стоимость 1 м2 для участков в несколько десятков гектар значительно ниже, чем стоимость 1 м2 участков для участков площадью несколько гектар.
В отчетах оценщиков часто встречается расчет корректировки на площадь с применением следующей формулы, рекомендуемой обычно [3] для оценки машин и оборудования:
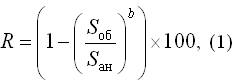
где
R — значение корректировки на площадь, %;
Sоб — площадь объекта оценки;
Sан — площадь аналога;
b — коэффициент торможения.
Значение коэффициента торможения авторы указанного выше источника рекомендуют выбирать в диапазоне 0,02…1,50, что при отличии площади объекта оценки от площади объекта-аналога на 10 % предполагает введение поправки от 0,2 до 14,6 %. Такой разброс недопустимо велик.
Для расчета коэффициент торможения (иногда называемого коэффициентом торможения параметра) применима следующая формула:
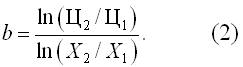
Расчет коэффициента торможения по этой формуле выполняют по двум аналогам, которые различаются только по одному (ценообразующему) параметру. В данном случае Ц1, Ц2 — цены объектов-аналогов; X1, X2 — площади объектов-аналогов.
Анализ формулы показывает, что для точного расчета коэффициента торможения необходимы аналоги с площадью, сопоставимой или приближенной к площади объектов оценки. На практике возникает описанная вначале проблема отсутствия аналогов, что также приводит к погрешности в расчетах, как и в расчете корректировок методом парных продаж.
Попробуем рассчитать корректировку с применением регрессионного анализа. В общем случае применение регрессионного анализа позволяет установить закономерность влияния основных ценообразующих факторов на результирующий показатель — стоимость объекта оценки. Однофакторный анализ можно провести в несколько этапов с применением MS Excel 2003.
Этап 1. Формирование выборки
Немаловажным условием формирования исходных данных является достоверность исходных данных. Муниципалитетом заключены договоры аренды подобных по функциональному назначению земельных участков. Информация о них получена оценщиком в муниципальном департаменте имущественно-земельных отношений. Условия сделок сопоставимы с условиями предполагаемой сделки, для которой определяется ставка: ставка годовой арендной платы y (зависимая переменная); площадь участка х (независимая переменная).
Таблица 1. Данные по прошедшим сделкам
| Площадь участка, м2 | Ставка годовой арендной платы, руб./м2 |
| 100 | 770 |
| 379 | 505 |
| 3 586 | 251 |
| 13 019 | 197 |
| 37 358 | 100 |
| 51 494 | 90 |
| 1 606 647 | 9 |
Этап 2. Определение подходящей зависимости
В анализе удобно использовать MS Excel 2003. В ячейки A1:B8 загружают исходные данные (табл. 1). Далее выделяют массив A1:B8 и выполняют последовательность команд: Главное меню / Вставка / Диаграмма / Точечная / Готово. В результате появляется диаграмма (рис. 1), на которой точками обозначены зависимости «Площадь/Ставка».
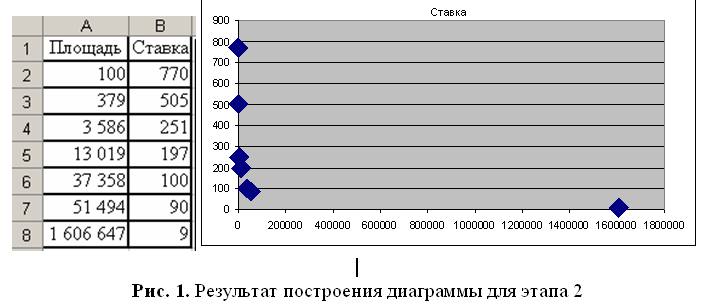
В классической учебной оценочной литературе большее внимание уделяется линейной зависимости, что вполне разумно и оправданно для оценки акций:
y = a + bx, (3)
где
b — наклон графика функции;
а — отрезок на оси y для прямой линии.
Если объекту присущи условно-постоянные затраты, выражающиеся в эффекте масштаба стоимостных характеристик, то линейная зависимость грубо и неадекватно будет характеризовать происходящее. Для фактических данных (см. рис. 1) зависимость является скорее степенной, нежели линейной:
y = axb, (4)
где
b — степень выпуклости/вогнутости графика функции;
а — смещение (масштаб) графика функции по оси ординат.
«Попросим» Excel вычислить параметры функции, наиболее правдоподобно описывающей зависимость по представленным исходным данным. Для этого щелкнем правой клавишей мыши по любой из точек значений построенной диаграммы (см. рис. 1, ромбики). Выберем «Добавить линию тренда… / Степенная». Перейдем на вкладку «Параметры», поставим флажки «Показать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации (R^2)»; нажмем кнопку ОК.
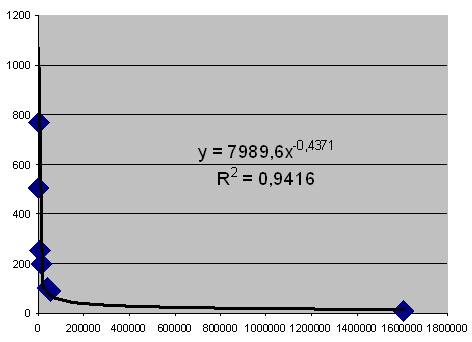
Достоверность полученной аппроксимации достаточно высока (наивысшая и практически недостижимая достоверность равна единице). Если в других случаях достоверность аппроксимации получена при подборе других функций, следует применять эти функции [4].
Этап 3. Преобразование модели
Для удобства продолжения расчетов в Excel без применения дополнительных средств целесообразно попытаться предложить компьютеру линейную модель. Полученная модель имеет вид (4): y = 7989,6x-0,4371. Функция нелинейна, однако, прологарифмировав ее по основанию е (постоянная Эйлера е = 2,718…), получим достаточно правдоподобное линейное представление:
y = axb → (5)
Для удобства можно сделать замену:
Y = ln y, X = lnx, A = ln a. (6)
После замены уравнение (5) выглядит следующим образом:
Y = A+ bX. (7)
В Excel поставим курсор в ячейку A10 и наберем =LN(A2). Затем протяжкой копируем формулы до B16 (поставим курсор в правый нижний угол ячейки A10; курсор превратится в крестик; потянем вниз и вправо). Получим вторую таблицу с преобразованными данными модели (рис. 3).
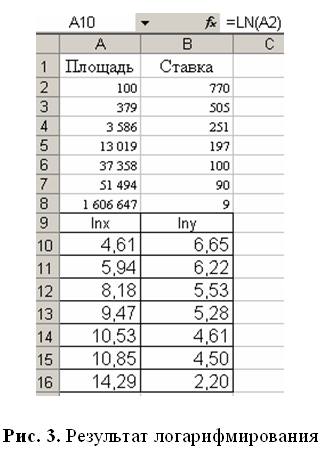
Этап 4. Подбор параметров линейной модели для преобразованных данных
Подбор параметров линейной модели удобно проводить стандартными средствами Excel. Проверим наличие таких средств: Главное меню / Сервис / Надстройки. Поставим галочки в пунктах «Пакет анализа», «Analysis ToolPak — VBA», нажмем кнопку ОК.
Запустим процедуру: Главное меню / Сервис / Анализ данных… / Регрессия / ОК.
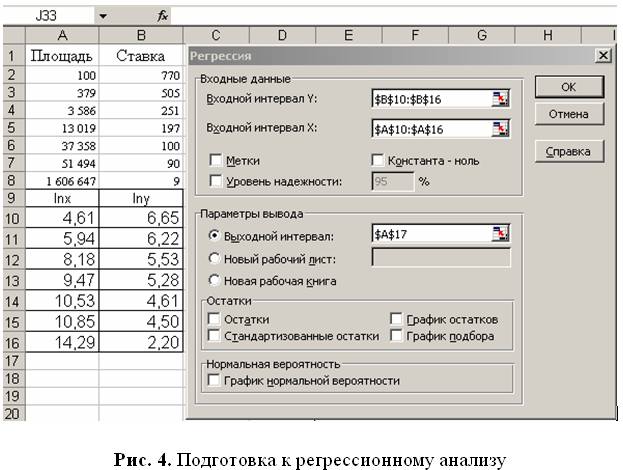
Следует указать входной интервал Y — $B$10:$B$16, входной интервал X -$A$10:$A$16, выходной интервал — $A$17. В результате получим вид, показанный на рис. 4. Нажмем кнопку ОК.
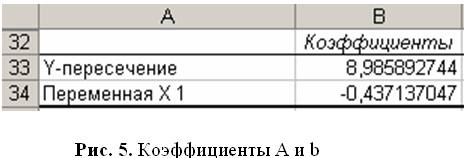
В ячейках В33:B34 находятся подобранные параметры модели: A=8,98; b=-0,43 (рис. 5).
Перед утверждением полученных данных необходимо проверить качество полученной модели.
Этап 5. Проверка качества подобранной модели
Качество преобразованной модели можно проверить стандартными средствами Excel, также представленными в полученной таблице. По критерию F= 80,6118, регрессия больше параметра «Значимость» F = 0,00028592.
Регрессионная статистика (рис. 6) показывает высокую вероятность верности предположения о наличии степенной зависимости пары «Площадь/Ставка».
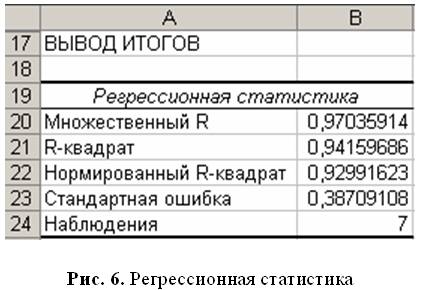
Множественный коэффициент корреляции R весьма высок — связь очень сильная. В этом можно удостовериться, сопоставив 0,97 с табличными данными (табл. 2) [5, с. 81].
Таблица 2. Сопоставление абсолютной величины коэффициента корреляции и характера связи
| Абсолютная величина коэффициента корреляции | Характер связи |
| До 0,2 | Практически отсутствует, слабая |
| От 0,2 до 0,3 | Умеренная |
| От 0,3 до 0,5 | Заметная |
| От 0,5 до 0,7 | Сильная |
| От 0,7 до 0,99 | Очень сильная |
Стандартная ошибка показывает отклонение фактических значений результирующего показателя от теоретической расчетной величины на удалении σ при распределении Гаусса, или (грубо) какой разброс данных присущ выборке.
Теснота связи параметров определяется по параметру R-квадрат (коэффициент детерминации), а для малых выборок, к которым относится и наш случай (7 наблюдений), целесообразно использовать нормированный R-квадрат (коэффициент детерминации, скорректированный на величину выборки). Эти данные свидетельствуют о тесноте связи имеющихся параметров и чем ближе его значение к единице, тем лучше модель описывает исходный ряд данных, т. е. из двух «хороших» моделей «победит» та, у которой нормированный R-квадрат выше.
Полученную модель можно считать достаточно достоверной.
Этап 6. Преобразование модели
В ячейках В33:B34 находятся подобранные параметры A=8,98; b=-0,43 (см. рис. 5). Подставим их в формулу (7):
Y = C+ bX → Y= 8,98 — 0,44X → lny = 8,98 — 0,44lnx.
Для восстановления данных необходимо применить потенцирование — нахождение числа по данному логарифму [6]:

Этап 7. Использование параметров в расчетах
В ячейки A37:A38 занесем площадь объекта оценки: 2350555 и 600444 м2 соответственно (рис.7). В ячейки B37:B38 запишем расчетные формулы, имея ввиду, что число e в Excel задается функцией =EXP(1).
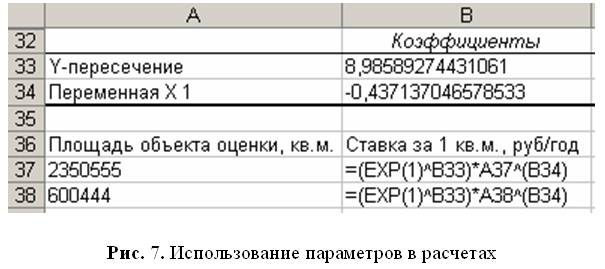
Более точными получаются расчеты с применением Excel. Обратите внимание, что разница между данными, рассчитанными на калькуляторе и с помощью Excel, может достигать 5 %. Поэтому в отчете целесообразно указывать использованные инструменты:
2,78,98 ´ 2350555-0,44 = 12 2,7182818288,985892744 ´ 2350555-0,437137047 = 13
Первый расчет выполнен на калькуляторе, второй — с помощью Excel.
В результате расчетов в Excel получена годовая ставка арендной платы одного квадратного метра для участка 2350555 м2 в размере 13,11 руб., а для участка 600444 м2 — 23,80 руб.
Литература
1. Федеральный стандарт оценки «Общие понятия оценки, подходы к оценке и требования к проведению оценки» (ФСО № 1), утвержден приказом МЭРТ РФ от 20 июля 2007 г. № 256, зарегистрирован в Минюсте РФ 22 августа 2007 г., регистрационный № 10040.
2. Лейфер Л.А. Точность результатов оценки и пределы ответственности оценщика. — http://www.labrate.ru/leifer/lev_leifer_accuracy_and_appraiser-s_liability-2009-1.htm
3. Ковалев А.П. Оценка стоимости активной части основных фондов. М.: Финстатинформ, 1998.
4. Елисеева И.И. Практикум по эконометрике. М: Финансы и статистика, 2006.
5. Грибовский С.В., Сивец С.А. Математические методы оценки стоимости недвижимого имущества. М.: Финансы и статистка, 2008.
6. Быковских А.М. Показательная и логарифмическая функции. Решение уравнений и неравенств. — http://window.edu.ru/window/library?p_mode=1&p_rid=49865&p_rubr=2.1.11